

Word Search
Get started
জয় শ্রী রাম
🕉Problem Statement:
Given an m x n board and a word, find if the word exists in the grid.
The word can be constructed from letters of sequentially adjacent cells, where "adjacent" cells are horizontally or vertically neighboring. The same letter cell may not be used more than once.
Example 1:
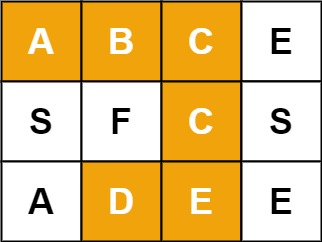
Input: board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "ABCCED"
Output: true
Example 2:
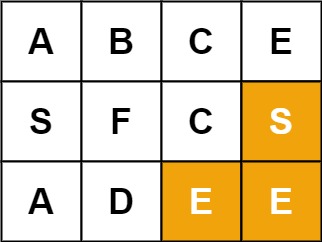
Input: board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "SEE"
Output: true
Example 3:
Input: board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "ABCB"
Output: false
Solution:
- NOTE: I highly recommend going through the Backtracking chapters in the order they are given in the Index page to get the most out of it and be able to build a rock-solid understanding.
If you have gone through Backtracking problems discussed previously, you already know how to solve this problem. For every candidate cell we would search all eligible adjacent cells, which is nothing but exhaustive searching. I won't go into details since we have already discussed that multiple times in previous chapters.
I would like to point out an important aspect that we need to take care of and often easy problems like this are asked in interviews to see how detail-oriented you are and if you are able to think of important yet simple things like this which would ultimately pay the most critical part in designing a correct algorithm and bug-free code: so the aspect here is that we cannot include a cell more than once while searching for a word. While searching for a word if a cell (x, y) is already visited as part of the current backtrack path (think of it as a path in the 'backtrack tree') we should not re-visit that again. Example: input: [["a", "a"]], string to search = "aaa", You cannot visit cell (0, 0) and (0, 1) and then again (0, 0) and say you found "aaa". Because (0, 0) is already visited you cannot revisit it.
Once you have figured this out, the rest would be super simple if you follow our backtracking template.
Java Code:
Login to Access Content
Python Code:
Login to Access Content
Don't forget to take in-depth look at the other backtracking problems because that is what would make you comfortable with using the backtracking template and master the art of Backtracking:
- Letter Case Permutation
- Power Set
- All Paths Between Two Nodes
- Sudoku
- N-Queens
- Word Square
- Generate Parentheses
