Graph Theory
Get started
জয় শ্রী রাম
🕉
We can represent graph in several ways as follows:
-
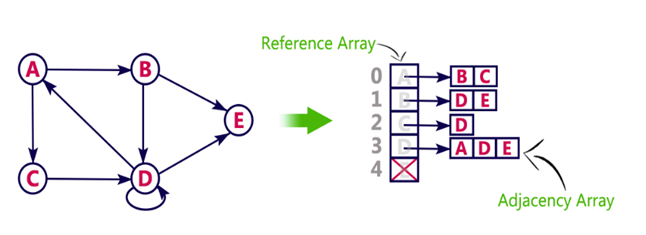
Adjacency List:
This is the way to go in solving real world problem in time and space efficient way, if you have the list of all the nodes present in the graph. Why do we need to know about the nodes in the graph ? Because the graph could be disconnected, as shown in the image above. If we are keeping an empty list as an adjacency list for a node that is connected to no other nodes then we would get to know what all nodes the graph has, if not, there is no way to know about the nodes with no inbound and outbound edges just from the adjacency list.
This is a versatile way of representing a graph and can be used to represent any kind of graph: Directed, Undirected, Weighted, Unweighted.
-
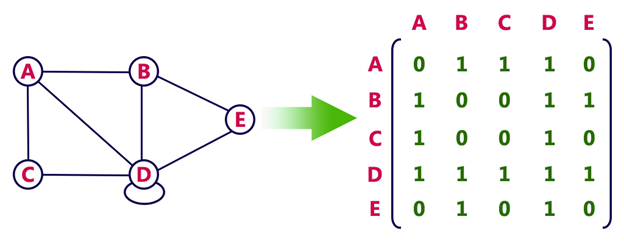
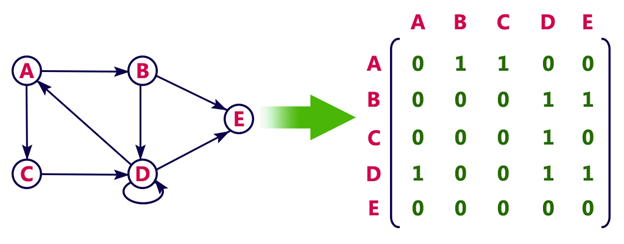
Adjacency Matrix:
One great thing about I find this useful for weighted graph, like problems involving Dijkstra's algorithm.
Otherwise, for unweighted directed or undirected graph I find myself using Adjacency List much more space and time efficient. Allocating space to store the whole n X n matrix, for n nodes, can often be a waste of space.
Also, for each node visited, to get its neighboring nodes you have to iterate over an entire row consisting of n nodes in the adjacency matrix. This could often be time inefficient.
In Adjacency Matrix, for a cell [i, j] we use 1 to indicate that there exists an edge nodes i and j, and 0 to denote that no edge exists in between the nodes i and j.
-
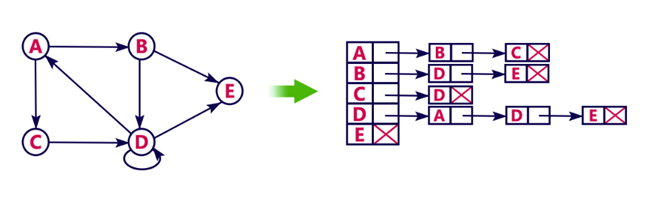
Edge List with information about any node which has no inbound or outbound edges:
From edge list you would often find yourself creating either an adjacency list or adjacency matrix. -
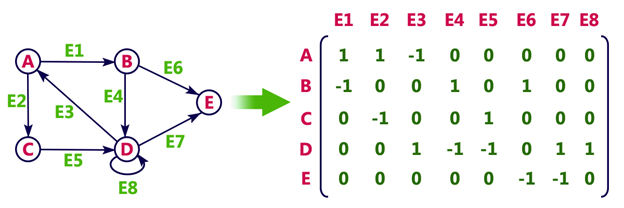
Incidence Matrix:
Incidence Matrix is used to represent Directed Graphs.