

Bipartite Graph
Get started
জয় শ্রী রাম
🕉A Bipartite Graph is a graph whose vertices can be divided into two independent sets, U and V such that every edge (u, v) either connects a vertex from U to V or a vertex from V to U. In other words, for every edge (u, v), either u belongs to U and v to V, or u belongs to V and v to U. We can also say that there is no edge that connects vertices of same set.
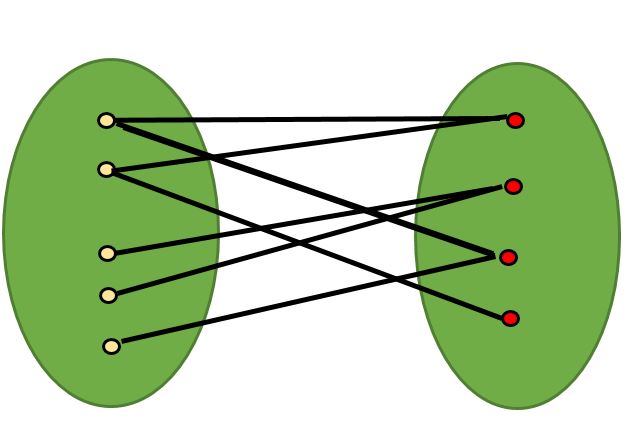
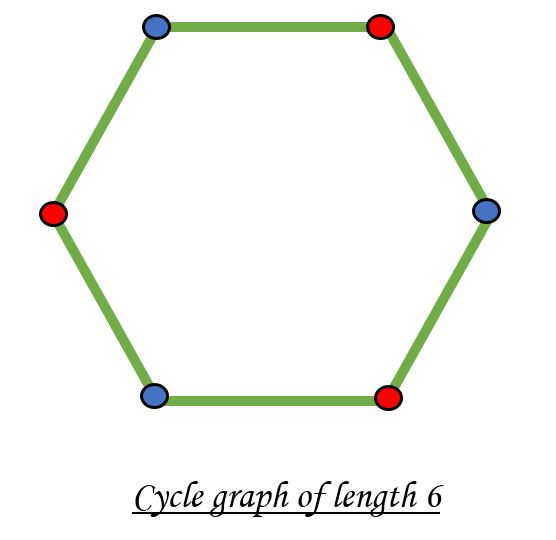
A bipartite graph is possible if the graph coloring is possible using two colors such that vertices in a set are colored with the same color. Note that it is possible to color a cycle graph with even cycle using two colors. For example, see the following graph.
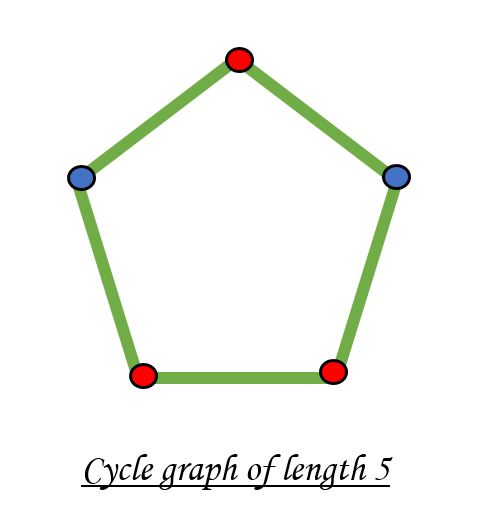
It is not possible to color a cycle graph with odd cycle using two colors.
Java Implementation:
1. Using BFS:
Algorithm to check if a graph is Bipartite:
One approach is to check whether the graph is 2-colorable.
Following is a simple algorithm to find out whether a given graph is Bipartite or not using Breadth First Search (BFS).
- Assign RED color to the source vertex (putting into set U).
- Color all the neighbors with BLUE color (putting into set V).
- Color all neighbor’s neighbor with RED color (putting into set U).
- This way, assign color to all vertices such that it satisfies all the constraints of m way coloring problem where m = 2.
- While assigning colors, if we find a neighbor which is colored with same color as current vertex, then the graph cannot be colored with 2 vertices (or graph is not Bipartite)
Java code:
Login to Access Content
Python Code:
Login to Access Content
2. Using DFS
The graph is given in the following form: graph[i] is a list of indexes j for which the edge between nodes i and j exists. Each node is an integer between 0 and graph.length - 1. There are no self edges or parallel edges: graph[i] does not contain i, and it doesn’t contain any element twice.Example 1:
Input: [[1,3], [0,2], [1,3], [0,2]]
Output: true
Explanation:
The graph looks like this:
0----1
| |
| |
3----2
We can divide the vertices into two groups: {0, 2} and {1, 3}.
Example 2:
Input: [[1,2,3], [0,2], [0,1,3], [0,2]]
Output: false
Explanation:
The graph looks like this:
0----1 | \ | | \ | 3----2
We cannot find a way to divide the set of nodes into two independent subsets.
Java code:
Login to Access Content
Python Code:
Login to Access Content
Related Topics:
- Graph Representation
- DFS
- Two End BFS
- Topological Sort
- Finding Cycles
- Cycle Detection Using DFS
- All Paths Between Two Nodes
