

Parallel Jobs Scheduling with Precedence and Relative Deadlines
Get started
জয় শ্রী রাম
🕉
Prerequisite:
Bellman-Ford Algorithm & Negative Cycle Detection
This is continuation of our last two chapters:
Here we will be further extending the problem discussed in Parallel Job Scheduling by adding one more type of constraint: Relative Deadline that specifies that a job must begin before a specified amount of time has elapsed relative to the start of another job.
So now the problem becomes:
We are given a set of jobs of specified duration to be completed, with precedence constraints that specify that certain jobs have to be completed before certain other jobs are begun. In addition, certain jobs must begin before a specified amount of time has elapsed relative to the start of another job. We can use as many processors as needed to execute jobs parallelly whenever we can. Write a program to compute if it is possible to execute all the jobs while still respecting all the constraints ?
Solution:
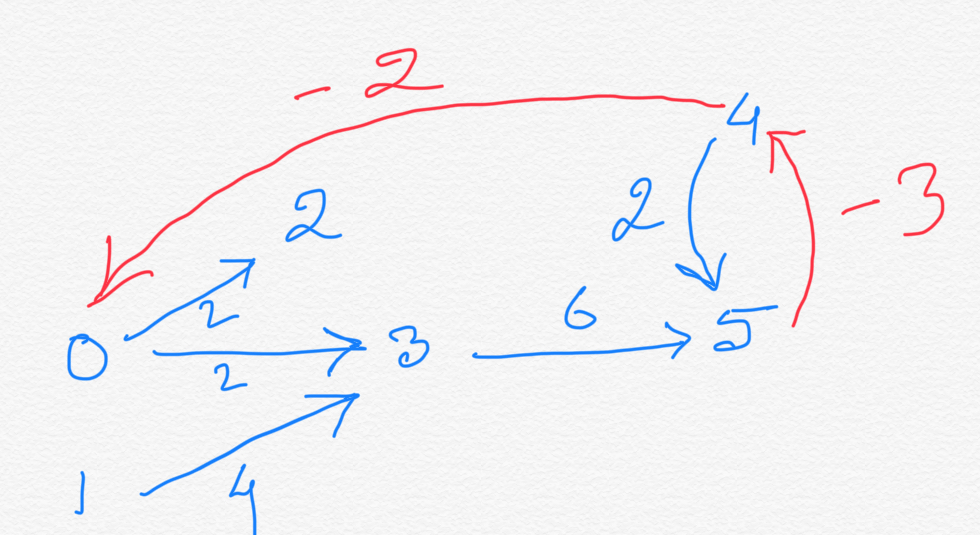
Let's take the same example as in Parallel Job Scheduling .Job id Duration Must complete after the completion of jobs # ------ -------- -------------------------------------------- 0 2 1 4 2 2 0 3 6 0 , 1 4 2 5 4 2 , 3, 4The graph we created was:
_ 2 ---(2)------
/| \
/(2) \
/ _\|
0 --(2)--> 3 --(6)---> 5
^ ^
| (4) | (2)
| |
1 4
We have the following constraints:
- 0 -> 2 and 0 -> 3, i.e, job 0 must complete before job 2 and 3,
- 1 -> 3, i.e, job 1 must complete before job 3
- 2 -> 5, i.e, job 2 must complete before job 5
- 3 -> 5, i.e, job 3 must complete before job 5
- 4 -> 5, i.e, job 4 must complete before job 5
- distance[0] = 0
- distance[1] = 0
- distance[2] = 2
- distance[3] = 2
- distance[4] = 0
- distance[5] = 8
So from distance[] array what we get is we can we can start job 0, 1 and 4 at the very beginning, parallelly, at the earliest. We cannot start job 2 and 3 before 2 unit time from beginning, and job 5 before 8 unit time from beginning. So the earliest we can start job 2 and 3 are 2 unit time from beginning. We can start job at 8 unit time starting from beginning at the earliest. Note that distance[i] gives the longest distance of vertex i from the source vertex.
Relative Deadline Constraint:
Now let's add the constraint specific to the problem we are solving here:- Job 5 must start no later than 3 time units after job 4 starts.
So now the question is, how can we represent this new constraint in the graph ?
Notice that all the edge weights in the above graph are meant for facilitating the computation of the earliest scheduling time of any job present in the graph. So we have a positive weight, say +d where d > 0, in a graph from vertex U to vertex V that indicates that job U takes d amount of time to complete, so job V can only start d amount of time after job U starts.Here the newly added constraint talks about the amount of time a job needs to start before another job. So, if we represent "time taken to start a job (v) after another job (u)" by positive weight edge from u to v, then "time a job (v) should start before another job (u)" should be negative weight edge from u to v.
So here you go. We have the answer now. Represent the relative deadline constraint by negative edges.
In our above example the jobs scheduling was still feasible even after adding the new relative deadline constraint. But that may not be the case all the time. Sometime adding certain relative deadline(s) constraint could make a job scheduling infeasible. Let's look at the below example:
Say, now we have one more relative deadline constraint:
- Job 0 must start no later than 4 time units after job 4 starts.
So now the problem boils down to : How to determine if a given set of constraints containing RELATIVE DEADLINES would result in a feasible Job Scheduling ? Let's think logically about the situation the "relative deadline" constraint creates, without drawing a graph first.
Say, distance[s] = d1 and distance[d] = d2 and job s must complete before job d does (If you are not familiar with distance[] array, please see Parallel Job Scheduling: Use Longest Paths Algorithm ). This means d1 is the earliest time job s can be scheduled, and job d can be scheduled at time d2 at the earliest. Clearly d2 > d1.
Now let's say d2 - d1 = d. This means: there needs to be at least d amount of time difference between the start of job s and job d.
Now let's see how relative deadline constraint look like:
Job d must start no later than X time units after job s starts.
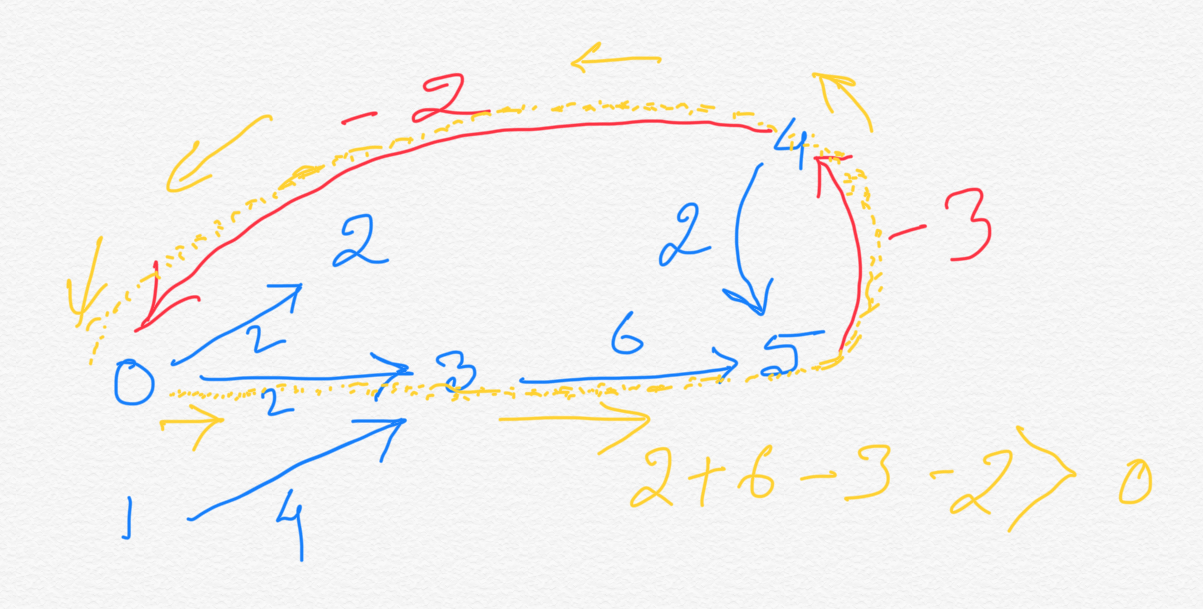
What value of X would make job scheduling impossible ? Since job s and job d need to be at least d time apart, job s cannot start X time before job d starts if X < d, because from start of job s to start of job d we at least need d amount of time to elapse. So, we have directed edge(s) from job s to job d, since job s must start before job d does. Due to the relative deadline constraint we now also have a negative weight edge (with weight = -X, where X > 0) from job d to job s. So, we have a cycle from job s to job d to back to job s. Since X < d in this case (we are discussing the situation where job scheduling becomes impossible due to relative deadline constraint) to sum of all the edges in the cycle = d + (-X) = d - X > 0 since X < d.
So a positive cycle (cycle with sum of the weights of all its edges > 0) would indicate that a job scheduling problem is not feasible with the given set of constraints.
On the other hand, if the earliest start times of job s and job d are d amount of time apart and job d needs to start after job s has started then a relative deadline constraint which says "Job d must start no later than X time units after job s starts." will NOT stop the job scheduling problem from being infeasible if X > d. Logically thinking, if the earliest time of job s and job d is at least d amount of time of time apart, to accommodate this new constraint all we have to do is delay the start of job d and it would meet this new constraint.
The graph below will illustrate the above discussion taking the example we have been using throughout this chapter:
Solution:
In the discussion above we saw that if we can find existence of a positive cycle in a graph we can say we have solved the problem of determining if a job scheduling problem is feasible given a set of relative deadline(s) constraints.
Now, in our chapter Bellman-Ford Algorithm & Negative Cycle Detection we have seen how we can detect existence of a negative cycle in a graph very efficiently using Bellman-Ford Algorithm
So let's negate all the edge weights and convert the solution from detecting positive cycle to detecting negative cycle and use Bellman-Ford Algorithm If we find a negative cycle in the modified (negated) graph, the job scheduling is impossible. Otherwise it is feasible. .
Problem Statement:
We are given a set of jobs of specified duration to be completed, with precedence constraints that specify that certain jobs have to be completed before certain other jobs are begun. In addition, certain jobs must begin before a specified amount of time has elapsed relative to the start of another job. We can use as many processors as needed to execute jobs parallelly whenever we can. Write a program to compute if it is possible to execute all the jobs while still respecting all the constraints ?Code Implementation:
Please subscribe to access the complete working solution.
After subscribing please come back and refresh this page.
Time Complexity:
Same as that of Bellman-Ford Algorithm: O(EV), in worst case E = V2 for dense graph. So if there are n jobs then the overall time complexity if O(n3).Summarization:
Sequential Job Scheduling: Use Topological Sort
Parallel Job Scheduling: Use Longest Paths Algorithm
Parallel Job Scheduling with Relative Deadline: Bellman-Ford Algorithm and Negative Cycle detection.
Related Must-Read Topics:
- Dijkstra's Algorithm
- Longest Paths Algorithm
- Topological Sort w/ Vertex Relaxation
- Bellman-Ford Algorithm & Negative Cycle Detection
- Optimized Bellman-Ford
- Sequential Job Scheduling
- Parallel Job Scheduling
- Arbitrage
